環の構造を調べる上で重要な準同型写像を紹介します。
環準同型写像(ring homomorphism)
2つの環 \(R,\ R^\prime\) に対して, 写像 \(f\ \colon\ R \to R^\prime\) が任意の \(x, y\in R\) と単位元 \(1\in R, 1^\prime\in R^\prime\) に対して
- \(f(xy)=f(x)f(y)\)
- \(f(x+y)=f(x)+f(y)\)
- \(f(1)=1^\prime\)
を満たすとき, \(f\) を \(R,\ R^\prime\) 間の環準同型写像(ring homomorphism)または単に準同型写像(homomorphism)という.
特に, \(f\) が全単射であるとき, 同型写像(isomorphism)といい,
\(R\) と \(R^\prime\) は(環として)同型(isomorphic) であるという.
\(R\) と \(R^\prime\) が同型であるとき, \(R\cong R^\prime\) と書く.
準同型の簡単な性質
\(f\ \colon\ R \to R^\prime\) を準同型写像, \(0, 0^\prime\) をそれぞれ \(R, R^\prime\) の零元とするとき, 以下が成り立つ.
- \(f(0)=0^\prime\)
- \(f(-x)=-f(x)\)
証明
\(f(0)=f(0+0)=f(0)+f(0)\) であるが, \(f(0)\) は \(R^\prime\) の元なので\(-f(0)\in R^\prime\).
\(-f(0)\) を両辺に加えると \(0^\prime=f(0)\) となる.
\(f(x)+f(-x)=f(x+(-x))=f(0)=0^\prime\) なので \(f(x)\) の和の逆元は \(-f(x)\).
よって \(-f(x)=f(-x)\).
例
実数上の1変数多項式環 \(\mathbf{R}[x]\) から実数 \(\mathbf{R}\) への写像 \[
\begin{eqnarray*}
f\ :\ \mathbf{R}[x]\quad&\longrightarrow&\quad\mathbf{R}\\
f(x)\quad&\longmapsto&\quad f(0)
\end{eqnarray*} \] は環の準同型写像です。

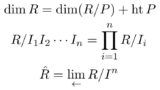
コメント