 不等式
不等式 ヘルダー平均の性質
\(-\infty\leq p\leq q\leq \infty\) を満たす \(p, q\) に対して \[M_p(x_1,x_2, \ldots,x_n)\leq M_q(x_1,x_2, \ldots,x_n)\] また \(p<q\) のとき, \[M_p(x_1,x_2, \ldots,x_n)=M_q(x_1,x_2, \ldots,x_n)\Longleftrightarrow x_1=x_2=\cdots=x_n\]
 不等式
不等式  不等式
不等式  不等式
不等式  不等式
不等式 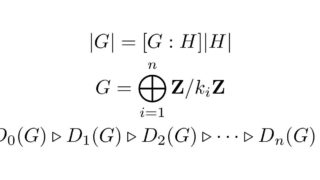 群
群 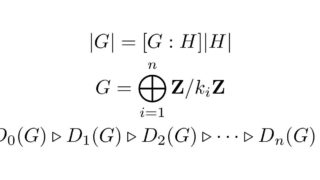 群
群 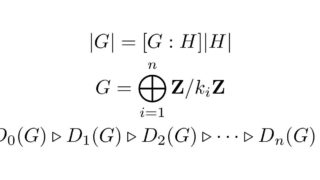 群
群