二項関係の中でも重要な概念である同値関係について紹介します。集合に対して、ある性質を持ったものをまとめて考える際によく用います。
集合 \(A\) 上の関係 \(R\) が同値関係(equivalence relation)であるとは
- 反射律 : 任意の \(a\in R\) に対して \(aRa\)
- 対称律 : \(a, b\in R\) に対して \(aRb \Longrightarrow bRa\)
- 推移律 : \(a, b, c\in R\) に対して \(aRb, bRc \Longrightarrow aRc\)
を全て満たすことをいう(反射的,対称的かつ推移的な二項関係を同値関係という).
同値関係を表すときには \(a\sim b, a\sim_R b, a\equiv b\) が良く使われる.
二項関係の定義的には \(R\) は \(A\times A\) 部分集合ですが、同値関係や順序関係を考えるときは、集合であることはあまり意識せず、関係演算子として考えた方が理解はしやすいと思います。
例1
任意の集合 \(A\) に対して元の相当関係 \(=\) は同値関係である.
例2
整数の集合 \(\mathbf{Z}\) とある正の整数 \(n\) を考える. \(a, b\in \mathbf{Z}\) に対して \(a-b\) を \(n\) で割ったときの余りが \(0\) であるとき, \(a\equiv b\) と定義する. このとき \(\equiv\) は \(\mathbf{Z}\) 上の同値関係となる.
通常, この \(\equiv\) は \(a\equiv b\ (\rm{mod}\ n)\) のように書かれ, \(a\) と \(b\) は \(n\) を法として合同であるという.
例3
\(n+1\) 次元のベクトル空間 \(\mathbf{R}^{n+1}\) に対して \(A=\mathbf{R}^{n+1}\setminus \mathbf{0}\) とおく. \(\mathbf{a},\mathbf{b} \in A\) に対して \(\mathbf{a}=r\mathbf{b}\) となる \(0\) でない実数 \(r\) が存在するとき \(\mathbf{a}\sim \mathbf{b}\) と定義すると, \(\sim\) は \(A\) 上の同値関係となる.
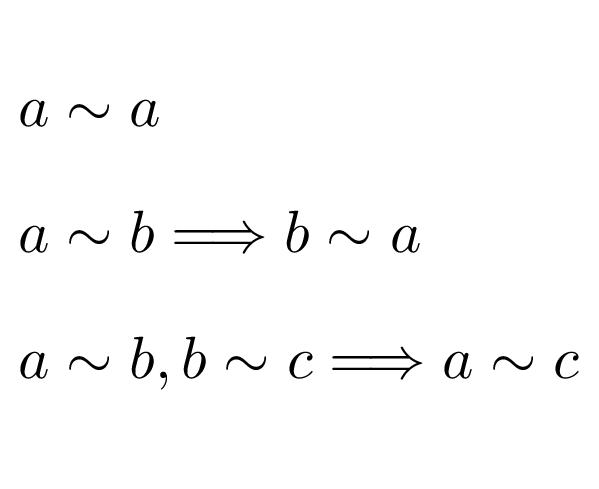
コメント