群において非常に重要な概念である正規部分群について紹介します。
正規部分群
群 \(G\) の部分群 \(N\) が
- \(\forall x\in G\ \ xNx^{-1}\subset N\)
を満たすとき, \(N\) を \(G\) の正規部分群(normal subgroup)といい \(N\triangleleft G\) や \(G\triangleright N\) と書く.
例
特殊線型群 \(SL_n(\mathbf{R})\) は一般線型群 \(GL_n(\mathbf{R})\) の正規部分群です。\(SL_n(\mathbf{R})\triangleleft GL_n(\mathbf{R})\).
実際, \(SL_n(\mathbf{R})=\{A\in GL_n(\mathbf{R})|\det A=1 \}\) でしたが,
任意の \(X\in GL_n(\mathbf{R})\) に対して, \(A\in SL_n(\mathbf{R})\) とすると
\[\det (XAX^{-1})=(\det X)(\det A)(\det X^{-1})=(\det X)(\det X^{-1})(\det A)=\det X\cdot \frac{1}{\det X}\cdot 1=1\]
となるので \(XAX^{-1}\in SL_n(\mathbf{R})\), つまり \(XSL_n(\mathbf{R})X^{-1}\subset SL_n(\mathbf{R})\) が分かります。
正規部分群であることを条件を整理します。
正規部分群の条件
群 \(G\) の部分群 \(N\) に対して次は同値である.
- \(N\) は \(G\) の正規部分群である(\(\forall x\in G\ \ xNx^{-1}\subset N\)).
- \(\forall x\in G\ \ xNx^{-1}=N\).
- \(\forall x\in G\ \ xN=Nx\).
証明
2と3が同値なのは明らか(\(xN\) などの定義から).
2\(\Longrightarrow\)1も明らかなので, 1\(\Longrightarrow\)2を示す.
\(\forall x\in G\ \ xNx^{-1}\subset N\) なので \(x\) を \(x^{-1}\) として見ても成立するから,
\(x^{-1}N(x^{-1})^{-1}=x^{-1}Nx\subset N\).
左から \(x\), 右から \(x^{-1}\) をかけて \(N\subset xNx^{-1}\). ゆえに \(xNx^{-1}=N\).

3番目が剰余群を考える上で重要になります。
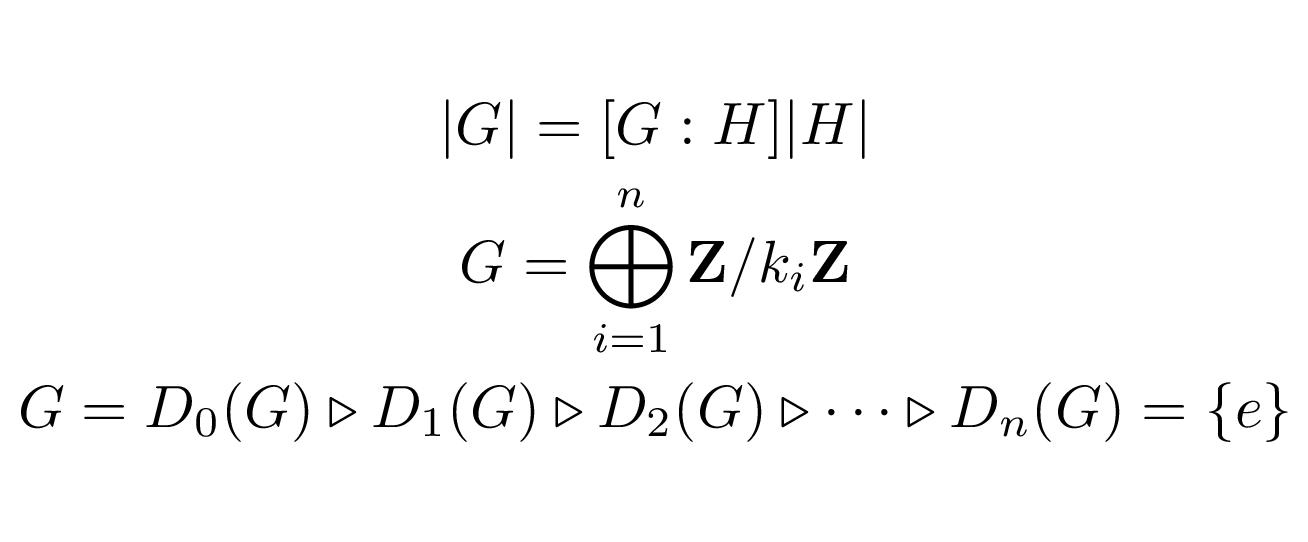
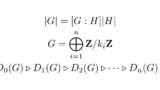
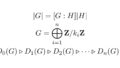
コメント