相加平均・相乗平均・調和平均の間には大小関係があります。
これらの関係は不等式の証明や値の評価で頻繫に使用されます。
証明はある関数を使うと比較的簡単にできます。
相加平均・相乗平均・調和平均の関係
\(n\) 個の正の実数 \(a_1,a_2, \ldots,a_n\) に対して, 以下が成り立つ:
\[\frac{a_1+a_2+\cdots+a_n}{n}\geq\sqrt[n]{a_1a_2\cdots a_n}\geq\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_n}}\]
つまり, 相加平均を \(A\), 相乗平均を \(G\), 調和平均を \(H\) とすると \[A\geq G\geq H\] が成り立つ.
\(a_1=a_2=\cdots=a_n\) の時のみ等号が成立し, \(A=G=H\) となる.
証明
(i) \(A\geq G\) を示す.
任意の実数 \(x\) に対して, \(e^x\geq x+1\) が成立する.
\(1\leq i\leq n\) なる \(i\) に対して \(x_i=\frac{a_i}{A}-1\) として \(x_i\) を先の不等式に代入すると \(e^{\frac{a_i}{A}-1}\geq \frac{a_i}{A}\) がわかる.
\(e^{\frac{a_i}{A}-1}\) と \(\frac{a_i}{A}\) は共に正であるから, \(i\) を \(1\leq i\leq n\) で動かしたものを全て掛け合わせると
\(e^{\frac{\sum_{i=1}^na_i}{A}-n}\geq \frac{\prod_{i=1}^na_i}{A^n}\)
となるが
\(\frac{\sum_{i=1}^na_i}{A}-n=\frac{\sum_{i=1}^na_i}{(\sum_{i=1}^na_i)/n}-n=n-n=0\)
なので
\(1=e^0\geq \frac{\prod_{i=1}^na_i}{A^n}\)
よって,
\(\displaystyle A^n\geq \prod_{i=1}^na_i\)
から \(A\geq G\) が従う.
また、\(e^x= x+1 \Leftrightarrow x=0\) より,
すべての \(i\) に対して \(x_i=0\) ならば \(A=G\).
一つでも \(x_i\neq 0\) となる \(i\) があれば \(A\geq G\) なので,
\(A \geq G\Leftrightarrow x_i=0\ (1\leq i\leq n)\Leftrightarrow a_1=a_2=\cdots=a_n\)
が分かる.
(ii) \(G\geq H\) を示す.
\(a_i\geq 0\) ならば \(\frac{1}{a_i}\geq 0\) なので \(\frac{1}{a_1},\frac{1}{a_2}, \ldots,\frac{1}{a_n}\) に対して(i)で示した相加平均と相乗平均の関係を使うと
\(\displaystyle \frac{\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_n}}{n}\geq \sqrt[n]{\frac{1}{a_1}\frac{1}{a_2}\cdots\frac{1}{a_n}}\)
となるが, 逆数を考えると
\(\displaystyle \frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_n}}\leq \sqrt[n]{a_1a_2\cdots a_n}\)
となり, これは \(H\leq G\) を表している.
等号成立は (i) の結果を使って
\(G \geq H\Leftrightarrow \frac{1}{a_1}=\frac{1}{a_2}=\cdots=\frac{1}{a_n}\Leftrightarrow a_1=a_2=\cdots=a_n\)
となる.
以上 (i) (ii) より, \(A\geq G\geq H\) であり, \(A=G=H\Leftrightarrow a_1=a_2=\cdots=a_n\) が分かる.
相加平均・相乗平均・調和平均の関係(2変数の場合)
正の実数 \(x,y\) の相加平均を \(A\), 相乗平均を \(G\), 調和平均を \(H\) とすると \[G^2=AH\] が成り立つ.
証明
\[A=\frac{x+y}{2},\ G=\sqrt{xy},\ H=\frac{2}{\frac{1}{x}+\frac{1}{y}}=\frac{2xy}{x+y}\]
より明らか.
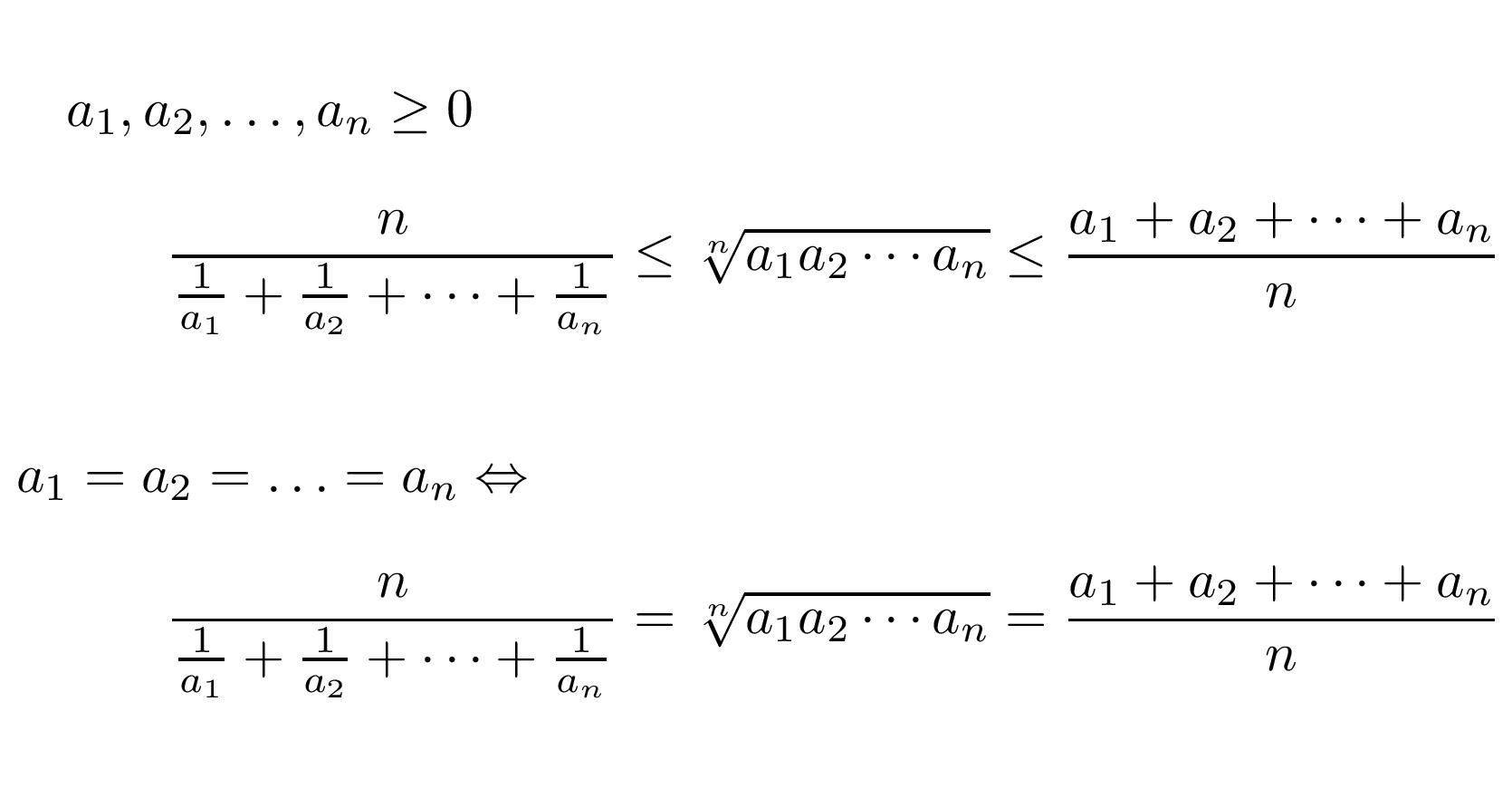

コメント