部分群の指数は群の構造を調べるのに役に立ちます。
指数に関する定理であるラグランジュの定理は、有限群の分類などで非常に強力な武器になります。
指数
\(G\) を群, \(H\) をその部分群とする.
\(G/H\) の基数(要素の数), つまり左剰余類の数を \(H\) の \(G\) における指数(index)といい, \((G:H),\ |G:H|,\ [G:H]\) などと表す.

\((G:H)=\infty\) となることもあります。
ラグランジュの定理
有限群 \(G\) の部分群 \(H\) に対して\[|G|=(G:H)|H|\] が成り立つ.
証明
\(a\in G\) に対して, 写像 \(H\rightarrow aH;x\mapsto ax\) を考える.
\(x, y\in H\) に対して, \(ax=ay\) とすると, \(a^{-1}\) を左からかけて \(x=y\). よって, 写像 \(H\rightarrow aH\) は単射.
全射は明らかなので, この写像は全単射となり, \(aH\) の要素数は \(|H|\) に等しいことが分かる.
また, 左完全代表系を \(\{a_\lambda\}_{\lambda\in\Lambda}\) とすると \(G=\bigcup_{\lambda\in\Lambda}a_\lambda H\) と書け, これは直和なので \(|G|=|\Lambda||H|\).
指数の定義より, \(|\Lambda|=(G:H)\) なので \(|G|=(G:H)|H|\) が成り立つ.
例1
\(G=\{e, g, g^2, g^3, g^4, g^5\}\) を位数 \(6\) の巡回群として, \(H=\{e, g^3\}\) とすると, \(H\) は \(G\) の部分群となります。
このとき, \(G/H=\{H, gH, g^2H\}\) であるから \((G:H)=3\) で \(|G|=(G:H)|H|\) が成立しています。
例2
\(G=GL_n(\mathbf{R}), H=SL_n(\mathbf{R})\) とします。
このとき, \(G/H=\{rH\ |\ r\in \mathbf{R}^\ast\}\) となっていて, \((G:H)=\infty\) です。
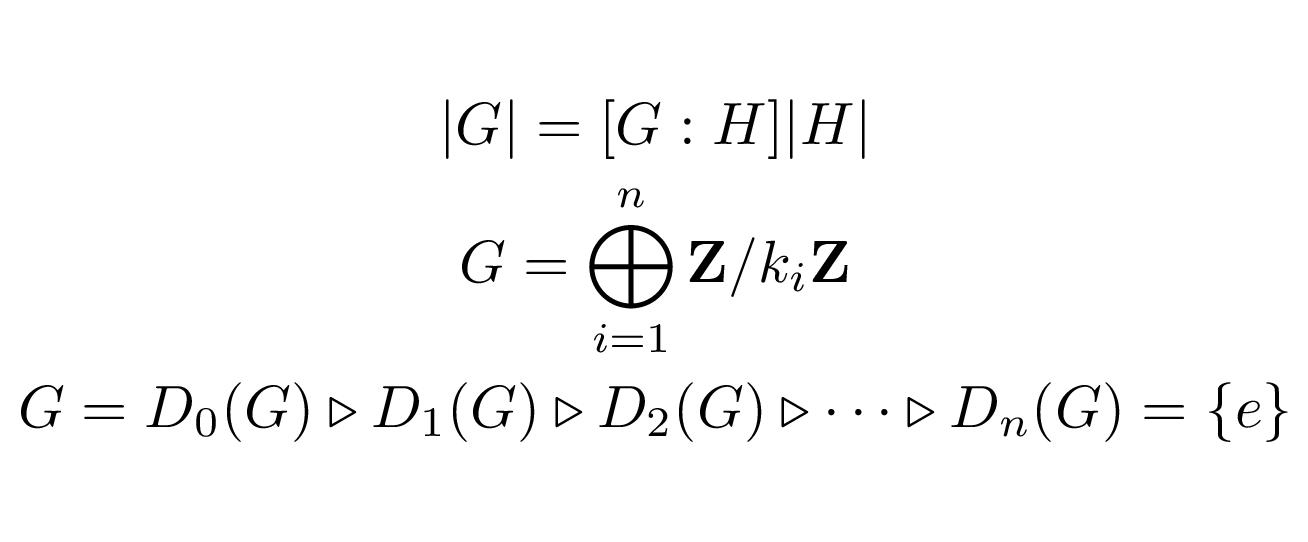

コメント