ここでは可換の場合を考えます。
グロタンディーク群
可換半群 \((S, +)\) に対して
半群の直積 \(S\times S\) 上の関係 \(\sim\) を \((m_1,n_1), (m_2,n_2)\) に対して
\(m_1+n_2+s=m_2+n_1+s\) なる \(s\in S\) が存在するとき \((m_1,n_1)\sim(m_2,n_2)\) と定義する.
\(\sim\) は半群合同である.
このとき \(G=S\times S/{\sim}\) 上の演算を, \((m,n)\) の同値類を \([m,n]\) と書くとき \[[m_1,n_1]+[m_2,n_2]=[m_1+m_2,n_1+n_2]\] で定義すると, 演算はwell-definedで \((G, +)\) はアーベル群である.
この \(G\) をグロタンディーク群(Grothendieck group)または\(K\)-群といい, \(K(S)\) と書く.
証明
\(\sim\) が同値関係であること.
反射律 : \(m_1+n_1+m_1=m_1+n_1+m_1\) なので \((m_1,n_1)\sim(m_1,n_1)\).
対称律 : \((m_1,n_1)\sim(m_2,n_2)\) のとき \(m_1+n_2+s=m_2+n_1+s\) となる \(s\) があるが,
\(m_2+n_1+s=m_1+n_2+s\) なので \((m_2,n_2)\sim(m_1,n_1)\).
推移律 : \((m_1,n_1)\sim(m_2,n_2),\ (m_2,n_2)\sim(m_3,n_3)\) のとき
\(m_1+n_2+s_1=m_2+n_1+s_1,\ m_2+n_3+s_2=m_3+n_2+s_2\) となる \(s_1, s_2\) があるが,
\[\begin{align*}
m_1+n_3+(s_1+s_2+n_2)
&=(m_1+n_2+s_1)+n_3+s_2\\
&=(m_2+n_1+s_1)+n_3+s_2\\
&=(m_2+n_3+s_2)+n_1+s_1\\
&=(m_3+n_2+s_2)+n_1+s_1\\
&=m_3+n_1+(s_1+s_2+n_2)\\
\end{align*}\] であるから \((m_1,n_1)\sim(m_3,n_3)\).
\(\sim\) が合同関係であること(\(G\) 上の演算がwell-definedであること).
\([m_1,n_1]=[m_1^\prime,n_1^\prime],[m_2,n_2]=[m_2^\prime,n_2^\prime]\) のとき,
\(m_1+n_1^\prime+s_1=m_1^\prime+n_1+s_1, m_2+n_2^\prime+s_2=m_2^\prime+n_2+s_2\) となる \(s_1, s_2\) があるが,
\[\begin{align*}
(m_1+m_2)+(n_1^\prime+n_2^\prime)+(s_1+s_2)
&=(m_1+n_1^\prime+s_1)+(m_2+n_2^\prime+s_2)\\
&=(m_1^\prime+n_1+s_1)+(m_2^\prime+n_2+s_2)\\
&=(m_1^\prime+m_2^\prime)+(n_1+n_2)+(s_1+s_2)
\end{align*}\] であるから \([m_1,n_1]+[m_2,n_2]=[m_1^\prime,n_1^\prime]+[m_2^\prime,n_2^\prime]\).
\(G\) がアーベル群であること
\(G\) は可換半群 \(S\times S\) の合同関係 \(\sim\) による剰余半群なので \(G\) は可換半群である.
任意の \(m,n,s,s^\prime\in S\) に対して \((m+s)+n+s^\prime=(n+s)+m+s^\prime\) であるから \([m,n]+[s,s]=[m+s,n+s]=[m,n]\).
よって \([s,s]\) は(加法の)単位元である.
また \([m,n]+[n,m]=[m+n,m+n]=[s,s]\) なので \([m,n]\) の逆元は \([n,m]\) である.
ゆえに \(G\) はアーベル群である.
例
自然数の全体 \(\mathbf{N}=\{0,1,2,3,\ldots\}\) は通常の加法で可換半群(モノイド)です。
\(\mathbf{N}\) のグロタンディーク群は整数全体 \(\mathbf{Z}=\{\ldots,-2,-1,0,1,2,\ldots\}\) になります。
詳しくは整数の定義の和の部分だけを見れば分かります。
普遍性
証明
\(i\,:\,S\to K(S)\) はある \(a\in S\) に対して \(m\mapsto [m+a,a]\) と定めても良い.
何故なら, 任意の \(a,b,m\in S\) に対して \([m+a,a]=[m+b,b]=[m+m,m]\) だからである.
以下 \(i\,:\,S\to K(S)\) を \(m\mapsto [m+a,a]\) とする.
\(m,n\in S\) に対して
\(i(m)+i(n)=[m+a,a]+[n+a,a]=[(m+n)+(a+a),a+a]=i(m+n)\)
となるので \(i\) は半群準同型である.
今, 半群準同型 \(f\,:\,S\to G\) が与えられたとする.
\(g\,:\,K(S)\to G\) を \(g([m,n])=f(m)-f(n)\) で定義する.(\(G\) は群なので \(f(n)\) の逆元が存在する)
\(g\) はwell-definedである.
well-definedであること
\([m,n]=[m^\prime,n^\prime]\) とすると
\(m+n^\prime+s=m^\prime+n+s\) となる \(s\) があるので
\(f(m)+f(n^\prime)+f(s)=f(m+n^\prime+s)=f(m^\prime+n+s)=f(m^\prime)+f(n)+f(s)\)
となり, アーベル群 \(G\) での演算なので移項して \(f(m)-f(n)=f(m^\prime)-f(n^\prime)\).
ゆえに \(g([m,n])=g([m^\prime,n^\prime])\).
\([m_1,n_1], [m_2,n_2]\in K(S)\) に対して
\[\begin{align*}
g([m_1,n_1]+[m_2,n_2])
&=g([m_1+m_2,n_1+n_2])\\
&=f(m_1+m_2)-f(n_1+n_2)\\
&=f(m_1)+f(m_2)-f(n_1)-f(n_2)\\
&=(f(m_1)-f(n_1))+(f(m_2)-f(n_2))\\
&=g([m_1,n_1])+g([m_2,n_2])
\end{align*}\]
なので \(g\) は群準同型である.
また, \(s\in S\) に対して
\(g(i(s))=g([s+a,a])=f(s+a)-f(a)=f(s)+f(a)-f(a)=f(s)\)
なので \(f=g\circ i\) である.
群準同型 \(h\,:\,K(S)\to G\) が \(f=h\circ i\) を満たしているとする.
\([m,n]+i(n)=[m+n+a,n+a]=[m,n]=i(m)\) より \([m,n]=i(m)-i(n)\) なので
\(h([m,n])=h(i(m)-i(n))=h(i(m))-h(i(n))=f(m)-f(n)=g([m,n])\)
となり, \(h=g\) が従う.
ゆえに \(g\) は一意的である.
簡約性と埋め込み
\(S\) を可換半群, \(K(S)\) をそのグロタンディーク群とする.
\(S\) が簡約的ならば \(i\,:\,S\to K(S)\,;\,m\mapsto [m+a,a]\) は単射準同型である.
証明
\(i(m)=i(n)\) のとき \([m+a,a]=[n+a,a]\) であるから
\((m+a)+a+s=(n+a)+a+s\) となる \(s\in S\) が存在するが,
\(S\) が簡約的なので \(m=n\) が従う.
ゆえに \(i\) は単射である.
この命題によって, \(S\) が簡約的可換半群ならば \(S\subset K(S)\) とみなせます。
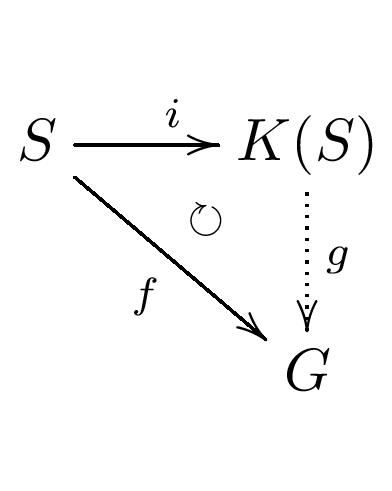
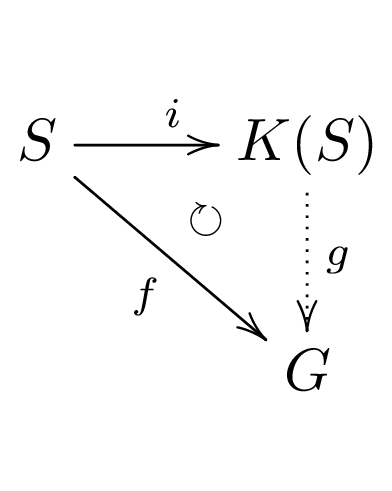

コメント