無限乗積を用いた円周率に関する公式
\[\sqrt{\frac{1}{2}}\,\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}}\,\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}}}\cdots = \frac{2}{\pi}\]
をビエト(Viète)の公式という.
証明
\(p_1(x)=\cos\displaystyle\frac{x}{2},\ p_n(x)=p_1(x)p_{n-1}\left(\displaystyle\frac{x}{2}\right)\ (n\geq 2)\) と置くと,
\[\begin{eqnarray*}p_2(x)&=&\cos\frac{x}{2}\cos\frac{x}{2^2}\\
p_3(x)&=&\cos\frac{x}{2}\cos\frac{x}{2^2}\cos\frac{x}{2^3}\\
&\vdots&\\
p_n(x)&=&\cos\frac{x}{2}\cos\frac{x}{2^2}\cos\frac{x}{2^3}\cdots\cos\frac{x}{2^n}
\end{eqnarray*}\]
となる. ここで \(\sin x\) に対して倍角の公式を繰り返し使うと,
\[\begin{eqnarray*}\sin x&=&2\cos\frac{x}{2}\sin\frac{x}{2}\\
&=&2^2\cos\frac{x}{2}\cos\frac{x}{2^2}\sin\frac{x}{2^2}\\
&=&2^3\cos\frac{x}{2}\cos\frac{x}{2^2}\cos\frac{x}{2^3}\sin\frac{x}{2^3}\\
&\vdots&\\
&=&2^n\cos\frac{x}{2}\cos\frac{x}{2^2}\cos\frac{x}{2^3}\cdots\cos\frac{x}{2^n}\sin\frac{x}{2^n}\\
&=&2^np_n(x)\sin\frac{x}{2^n}
\end{eqnarray*}\]
なので
\[p_n(x)=\frac{\sin x}{2^n\sin\displaystyle\frac{x}{2^n}}\]
よって
\[\lim_{n\rightarrow \infty}\ p_n(x)=\lim_{n\rightarrow \infty}\ \frac{\sin x}{2^n\sin\displaystyle\frac{x}{2^n}}=\lim_{n\rightarrow \infty}\ \frac{\displaystyle\frac{x}{2^n}}{\sin\displaystyle\frac{x}{2^n}}\frac{\sin x}{x}=\frac{\sin x}{x}\]
これより
\[\lim_{n\rightarrow \infty}\cos\frac{x}{2}\cos\frac{x}{2^2}\cos\frac{x}{2^3}\cdots\cos\frac{x}{2^n}=\frac{\sin x}{x}\]
ここに \(x=\displaystyle\frac{\pi}{2}\) を代入すると
\[\lim_{n\rightarrow \infty}\cos\frac{\pi}{2^2}\cos\frac{\pi}{2^3}\cos\frac{\pi}{2^4}\cdots\cos\frac{\pi}{2^{n+1}}=\frac{2}{\pi}\]
である. \(\cos\displaystyle\frac{\pi}{2^2}=\sqrt{\frac{1}{2}}\) であり, 半角の公式より \(\cos\displaystyle\frac{\pi}{2^k}=\sqrt{\frac{1}{2}+\frac{1}{2}\cos\displaystyle\frac{\pi}{2^{k-1}}}\) なので
\[\begin{eqnarray*}\cos\frac{\pi}{2^3}&=&\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}}\\
\cos\frac{\pi}{2^4}&=&\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}}}\\
&\vdots&
\end{eqnarray*}\]
これらを代入して
\[\sqrt{\frac{1}{2}}\,\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}}\,\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}}}\cdots = \frac{2}{\pi}\]
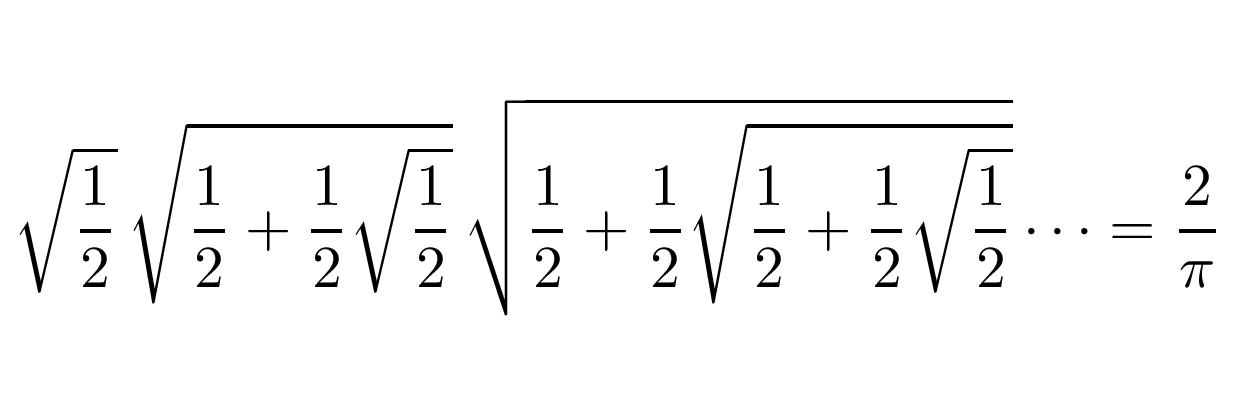
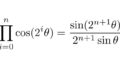

コメント