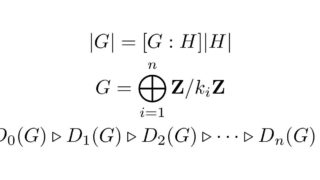空積

\(S_1,S_2\) を半環として, \(0_1,0_2\) をそれぞれの零元, \(1_1,1_2\) をそれぞれの単位元とする. 集合としての直積 \[S_1\times S_2=\left\{\ (s_1,s_2)\ |\ s_1\in S_1,\ s_2\in S_2\ \right\}\] 上に二項演算 \(+\) と \(\cdot\) を \((s_1,s_2),\ (s_1^\prime,s_2^\prime)\in S_1\times S_2\) に対して \[ (s_1,s_2)+(s_1^\prime,s_2^\prime)=(s_1+s_1^\prime,s_2+s_2^\prime)\\ (s_1,s_2)\cdot (s_1^\prime,s_2^\prime)=(s_1s_1^\prime,s_2s_2^\prime) \] で定義すると \(S_1\times S_2\) は半環となる. この半環を \(S_1,S_2\) の直積(direct product)という. \(S_1\times S_2\) の零元は \((0_1,0_2)\), 単位元は \((1_1,1_2)\) である.