 環
環 局所化
\(R\) を可換環, \(S\) を \(R\) の積閉集合とする.\((a,s), (b,t) \in R\times S\) に対して, ある \(u\in S\) が存在して \(u(at-bs)=0\) となるとき
\((a,s)\sim (b,t)\) と定義すると \(\sim\) は \(R\times S\) 上の同値関係となる.
 不等式
不等式  不等式
不等式 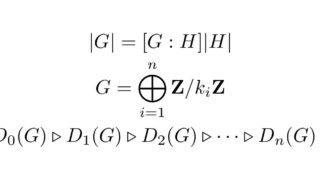 群
群