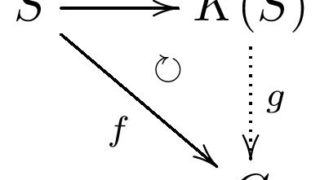
群 グロタンディーク群
半群から、それを”含む”ような群を構成できます。
可換半群 \((S, +)\) に対して半群の直積 \(S\times S\) 上の関係 \(\sim\) を \((m_1,n_1), (m_2,n_2)\) に対して
\(m_1+n_2+s=m_2+n_1+s\) なる \(s\in S\) が存在するとき \((m_1,n_1)\sim(m_2,n_2)\) と定義する.
\(\sim\) は半群合同である.
2022-07-21
群 
半群 半群の直積
\(S_1,S_2\) を半群とする.
集合としての直積 \[S_1\times S_2=\left\{\ (s_1,s_2)\ |\ s_1\in S_1,\ s_2\in S_2\ \right\}\] 上に二項演算 \(\cdot\) を \((s_1,s_2),\ (s_1^\prime,s_2^\prime)\in S_1\times S_2\) に対して \[
(s_1,s_2)\cdot (s_1^\prime,s_2^\prime)=(s_1s_1^\prime,s_2s_2^\prime)
\] で定義すると \(S_1\times S_2\) は半群となる.
この半群を \(S_1,S_2\) の直積(direct product)という.